- جایزه انجمن فیزیک ایران
- جایزه حسابی
- جایزه دبیر برگزیده فیزیک
- جایزه ساخت دستگاه آموزشی
- جایزه صمیمی
- جایزه توسلی
- جایزه علی محمدی
- پیشکسوت فیزیک
- بخش جوایز انجمن
نقشههای سهبعدی از ضریب شکستِ یک نمونه، که در برخی از آزمونهای بیوپزشکی استفاده می شوند را میتوان مستقیماً از اندازهگیریهای وابسته به زاویهی پراکندگی نور از آن نمونه بدست آورد.
ضریب شکست مهمترین ویژگی اپتیکی بزرگمقیاس از یک ماده است. این ضریب، طولموج موثر نور و مسیرحرکت آن را در درون ماده مشخص میکند. دستکاری ضریب شکست میتواند مسیر حرکت نور را به روشهای شگفتانگیز (همانطور که در شبهمواد دیده شده است) دستخوش تغییر کند [1] یا رفتار گسیلندههای جاسازی شده را بطور چشمگیری تغییر دهد [2]. با این حال گسترهی ضریب شکست فراتر از دستکاریهای نوری است: ضریب شکست ممکن است به چگالی جرمی و ویژگیهای مکانیکی و الکتریکی یک محیط نیز ارتباط پیدا کند. این رابطه باعث میشود تا این ضریب، نشانگر زیستی مفیدی برای مطالعهی سلولهای زیستی بهحساب آید. پژوهشگران با اندازهگیری ضریب شکست در یک نمونه قادرند بیماریهایی همچون مالاریا را تشخیص دهند یا ویژگیهای اصلی تکسلولهای زیستی را مشخصهیابی کنند [3]. اکنون آنتونیو فیوره (Antonio Fiore) از دانشگاه مریلند در کالج پارک و همکارانش رهیافت بدون-برچسبی برای نقشهبرداری از ضریب شسکت نمونهها با وضوح فضایی بالا و در سه بعد را به اثبات رساندهاند [4]. این روش از اندرکنش نور با ارتعاشات حرارتی ذاتی (فونونها) استفاده میکند؛ اندرکنشی که وابسته به زاویه است. این روش جدید در مقایسه با روشهای موجود، اندازهگیری مستقیمی از ضریب شکست را بدون نیاز به هیچ دانش یا فرضی در مورد ویژگیهای هندسی و اپتیکی نمونه فراهم میکند.
با این حال فناوریهای موجود محدودیتهایی نیز دارند: برای مثال این فناوریها نیازمند دانش اولیه در مورد هندسهی نمونهها، اتکا بر فرضهایی معین درمورد ویژگیهای اپتیکی ماده یا نیازمند مقایسهی اندازهگیریها با مقادیر تداخلی هستند که همهی آنها را نمیتوان به سادگی برای نمونههای پیچیده انجام داد. این فناوریها همچنین در معرض مصنوعات موسوم به بسته فازی قرار گرفتهاند: الگوهای بازسازی شدهی ساختگی از ضریب شکست زمانی نتیجه میدهند که تغییرات فاز نور تصویربرداری در داخل نمونه بزرگ بوده یا یکنواخت نباشد. این رهیافت که توسط فیوره و همکارانش پیشنهاد شده به شکل بالقوهای به برخی از این محدودیتها که بواسطهی فراهم کردن راهی مستقیمتر برای اندازهگیری ضریب شکست نور در طی اندرکنش نور با امواج صوتی است، غلبه میکند. این فناوری جدید بر پایهی روش اسپینترونیکی است که پراکندگی نور بریلوئنِ همزمان نام دارد. این روش شامل پویش یک نمونه با یک لیزر تکبسامد و اندازهگیری نور پراکندهشده از نمونه به شکل غیرکشسان است یعنی با بسامدی متفاوت از لیزر فرودی. این سیگنالها از پراکندگی غیرکشسان از جفتشدگی نور با فونونهای آکوستیکی نتیجه میشوند[9].
در یک آزمایش بریلوئنِ عادی میتوان دو قله (پیک) غیرکشسان را در نور پراکنده شده مشاهده کرد که قلههای استوکس و ضداستوکس نام دارند. این قله ها اندکی به لحاظ بسامد در حول و حوش قلههای پراکندگی کشسان اصلی قرار دارند. با در نظر داشتن انرژی پایین مدهای فونونی آکوستیک، این دو قله به لحاظ طیفی به قله پراکندگی کشسان بسیار نزدیک هستند با یک جابجاییِ عادی که برای نمونههای زیستی در طولموجهای اپتیکی از مرتبهی ۱۰ گیگاهرتز است. این جابجاییِ بسامدی که متناسب با سرعت فونون آکوستیکی پویششده است را میتوان به عنوان ظهور جابجایی دوپلر در نظر گرفت: ناشی از نوری که توسط فونونهای متحرک پراکنده میشود.
ایدهی اصلی پشت این رهیافت آن است که ضریب شکست نمونه را میتوان با پویش پراکندگی بریلوئن در هندسههای دوبعدی نقشهبرداری کرد. اولین هندسه یک هندسهی پسپراکندگی یا هندسهی صفر است که در آن جهت فوتونهای فرودی و پراکنده شده تقریباً در خلاف هم است (شکل 1a). در ترکیببندی دوم یا هندسهی آلفا، هرکدام از نورهای فرودی و پراکندهشده تقریباً در زاویهی آلفا نسبت به عمود به سطح قرار دارند (شکل 1b). جابجایی قلههای بریلوئن در هندسهی آلفا متفاوت از جابجایی در هندسهی صفر است. نویسندگان این پژوهش عبارات تحلیلی برای این جابجاییها بدست آورده و نشان دادهاند که هردوی این ترکیببندیها، فونونهای آکوستیکی منتشر شده در طول یک محور یکسان را پویش میکنند. محاسبات آنها از رابطهی مابین نسبت جابجاییها و ضریب شکست در حجم پویششده در نقطهی کانونی پرده برداشته است:
n=(sin2α/1-R2)1/2
بنابراین این تیم با اندازهگیری جابجاییهای بریلوئن قادر شدهاند تا مستقیماً ضریب شکست را در درون حجمی که فوتونها پراکنده میشوند، استخراج کنند.
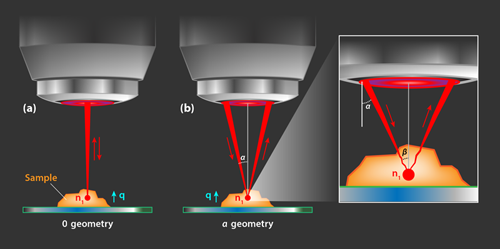
شکل۱) طرحی از روش نقشهبرداری ضریب شکست که توسط فیوره و همکارانش به اثبات رسیده است. این روش بر پایهی استفاده از یک میکروسکوپ کانونی برای تصویربرداری از نور پراکنده شده از نمونه در دو هندسه است. a) در هندسهی صفر، فوتونهای فرودی و پراکنده شده به بین سطحی عمودند b) در هندسهی آلفا نور فرودی و پراکندهشده زاویهی متوسط آلفا را نسبت به عمود بین سطحی میسازند. چون هردوی هندسهها جهت فونونی یکسان دارند (q) جابجایی بسامد بریلوئن اندازهگیریشده (که به زاویهی داخلی بتا وابسته است) را میتوان به ضریب شکست در نقطهی کانونی ارتباط داد.
فیوره و همکارانش این رهیافت را برای یک میکروسکوپ کانونیِ پویشگر پیادهسازی کردهاند. میکروسکوپ کانونی، تصاویری سهبعدی را با انجام اندازهگیریهای مستمر در نقطهی کانونی تولید میکند که در طول حجم یک نمونه پویش شده است. پژوهشگران با استفاده از سیستمی از آینههای فلیپ و شاترها میتوانند پراکندگی بریلوئن در هندسههای صفر و آلفا را سریعاً تعویض کنند. آنها از یک «طیفسنج آرایهای فاز با تصویر مجازی» برای اندازهگیری جابجاییهای کوچک در این جابجاییهای سریع استفاده میکنند. برای اعتبارسنجی این رهیافت نشان دادهاند که میتوان از ضریب شکست یک قطرهی پلیمری که توسط نور فعالشده و بر روی یک ظرف پتری قرار دارد، نقشههای سهبعدی فضایی دقیق بدست آوردند.
این محققان وضوح فضایی با چند میکرومتر را در سه بعد نشان دادهاند. در تصویربرداری از یک نمونهی واقعی، وضوح تصویر به درجهی همپوشانیِ کانونی برای دو جهت پویشی (صفر و آلفا) بستگی خواهد داشت که اثبات آن بهویژه برای کنترل عمیق در درون نمونههایی با تغییرات ضریب شکست قابلملاحظه چالش برانگیز است. در چنان مواردی میتوان از اپتیک تنظیمپذیر دیگری استفاده کرد تا از همپوشانی کانونیِ سازگار مطمئن شد. با بکارگیری دیگر ترفندها مثل دیافراگم بزرگتر و ترکیببندیهای مختلف از عدسیها، پژوهشگران یک وضوح فضایی زیر میکرومتر را پیشنهاد دادهاند که در تمامی ابعاد قابل دسترس است. با این حال بهبود وضوح فضایی ممکن است دقت اندازهگیری طیف بریلوئن را تحت تاثیر قرار دهد که به نوبهی خود دقت تعیین ضریب شکست را کاهش میدهد. همانگونه که نویسندگان این پژوهش اشاره کردهاند، این کاهش میتواند با انجام اندازهگیریها بر روی بیش از دو زاویه تخفیف پیدا کند اما این کار چالشهای دیگری را نیز بهوجود میآورد. سرانجام یافتن توافقی مابین پیچیدگیهای تجربی و دقت مطلوب ضریب شکست و وضوح فضایی لازم خواهد بود.
علیرغم پیچیدگی این آزمایش، پیشرفتهای آینده در طیفسنجهای بریلوئن میتواند به پیادهسازیهای گسترده از رویکرد مفهوم و ظریفی که توسط این پژوهشگران به اثبات رسیده، منجر شود. چون این رهیافت بدون برچسب است (یعنی به اضافهکردن نشانگرهای فلورسنتی یا دیگر نشانگرها نیازی ندارد) بهویژه در کاربردهای تصویربرداری زیستی و تشخیصی جذاب خواهد بود. به همین ترتیب میتوان برای مثال از آن، جهت تحلیل رفتار چگالی جرمی سلولی که به توسعهی سرطان مربوط است و یا آسیبهای قرنیه استفاده کرد.
این پژوهش در مجلهی فیزیکال ریویو لترز انتشار یافته است.
مراجع:
- H. Chen, C. T. Chan, and P. Sheng, “Transformation optics and metamaterials,” Nat. Mater. 9, 387 (2010).
- E. M. Purcell, “Resonance absorption by nuclear magnetic moments in a solid,” Phys. Rev. 69, 681 (1946).
- P. Y. Liu et al., “Cell refractive index for cell biology and disease diagnosis: past, present and future,” Lab Chip 16, 634 (2016).
- A. Fiore, C. Bevilacqua, and G. Scarcelli, “Direct three-dimensional measurement of refractive index via dual photon-phonon scattering,” Phys. Rev. Lett. 122, 103901 (2019).
- E. Abbe, Neue Apparate zur Bestimmung des Brechungs - und Zerstreuungsvermögens fester und fluüssiger Körper (Mauke's Verlag, Jena, 1874).
- Y. Park, C. Depeursinge, and G. Popescu, “Quantitative phase imaging in biomedicine,” Nat. Photon.12, 578 (2018).
- X. J. Liang, A. Q. Liu, C. S. Lim, T. C. Ayi, and P. H. Yap, “Determining refractive index of single living cell using an integrated microchip,” Sens. Actuators A 133, 3354 (2007).
- C. Tregidgo, J. A. Levitt, and K. Suhling, “Effect of refractive index on the fluorescence lifetime of green fluorescent protein,” J. Biomed. Opt. 13, 031218 (2008).
- B. J. Berne and R. Pecora, Dynamic Light Scattering With Applications to Chemistry, Biology, and Physics (Dover Publications Inc., Mineola, 2000)[Amazon][WorldCat].
دربارهی نویسنده:
کریم الصیاد (Kareem Elsayad) سرتیم میکروسکوپ پیشرفته در موسسهی تجهیزات هستهی مرکز زیستی وین در اتریش است.
منبع:
A New Angle on Mapping the Refractive Index
نویسنده خبر: بهنام زینالوند فرزین
آمار بازدید: ۳۲۰
ارجاع دقیق و مناسب به خبرنامهی انجمن بلا مانع است.»
 RSS
RSS