- جایزه انجمن فیزیک ایران
- جایزه حسابی
- جایزه دبیر برگزیده فیزیک
- جایزه ساخت دستگاه آموزشی
- جایزه صمیمی
- جایزه توسلی
- جایزه علی محمدی
- پیشکسوت فیزیک
- بخش جوایز انجمن
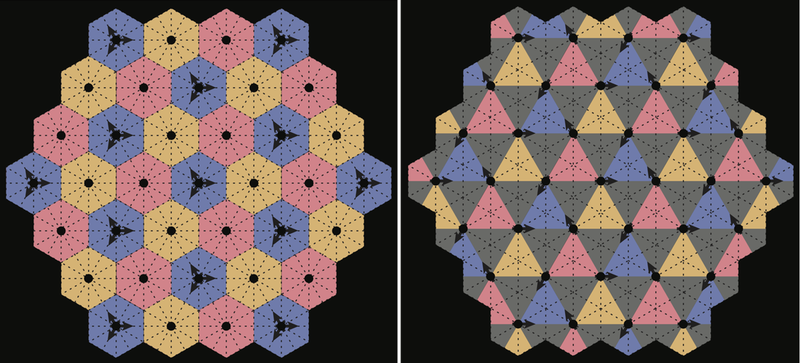
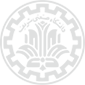
نظریهپردازان نوع جدیدی از کریستالها را تعریف کردند که تقارن آنها بر اساس قرار گرفتن اجسام در جایگاههای ثابت نیست، بلکه مبنای آن رابطه میان حرکتهای تناوبی آنها، همانند مجموعهای از ماهوارههاست.
کریستالها معمولاً به صورت آرایههای منظمی از مولفههای ثابت و ساکن، مانند اتمها و مولکولها تعریف میشوند. اما پژوهشگران شکل جدیدی از کریستالها را پیشنهاد دادهاند که در آن این نظم و ترتیب در قالب جابهجاییهای هماهنگ و موزون مولفهها، مانند حرکت ماهوارهها تعریف میشود. این گروه پژوهشی، مجموعههای این چنینی را «کریستالهای رقصان» نامیدند و نظریهای رسمی برای تعریف و مشخصهیابی آن تدوین کردند.
لاتام بویل از موسسه فیزیک نظری پریمیتر در واترلو کانادا میگوید در همان زمان که شروع به اندیشیدن درباره این مساله کرده بود، برنامههایی را هم برای رصد فضایی به منظور یافتن امواج گرانشی در ذهن داشت. رصد پیشنهادی از سه ماهواره که به دور خورشید میگشتند، استفاده میکرد. بنابراین آنها همواره در سطحی هموار محصور بودند. بویل دریافت که اگر از چهار ماهواره استفاده کنند میتوانند علامتهای بیشتری از امواج گرانشی را دریابند، زیرا دیگر نیازی نیست که همه ماهوارهها در همان سطح هموار همیشگی قرار گیرند.
اگرچه هیچ کس تصمیم ساختن چنین مجموعهای را نداشت، ولی بویل متعجب بود که اگر چرخش چهار ماهواره را بتوان به گونهای متقارن هماهنگ کرد، فیلمهایی که این چهار ماهواره ضبط میکنند، باید یکسان باشند. هماکنون وی به همراه همکارانش حرکت این چهار-ماهواره را به صورت ریاضی شرح میدهد. هر چهار ماهواره حول یک نقطه مرکزی یکسان دور میزنند و به صورت موازی در یکی از وجههای چهاروجهی منتظم میچرخند. زمانبندی نسبی به گونهای است که به نظر میرسد هر یک از آنها در هر چرخش شش مرتبه در گوشه یک مربع قرار میگیرند. بویل میگوید: این مجموعه چرخشها «آشکارا جسم هندسی بسیار ویژه و زیبایی را میسازد که به نوبه خود جالب توجه است و میتوان آن را نمونهای دینامیکی برای چهاروجهی منتظم دانست».
پژوهشگران برای عمومیسازی نتیجهی چهار-ماهواره از نظریه عملیات تقارن استفاده میکنند و پیکربندیهای منظم دیگری را امتحان میکنند که در آنها «دستههایی» با تعداد دلخواه از ماهوارهها وجود دارد. آنها کمیتی با نام «رقصآرایی» (خطای پردازش ریاضی) را تعریف میکنند که مقیاسی است برای نشان دادن میزان تقارن موجود در میان ذرات که در حال چرخش تناوبی هستند. برای مثال، تصور کنید دو اسکیتباز به طور همزمان از شمال-به-جنوب و از شرق-به-غرب در طول مرکز میدان مربعشکلی در حرکتاند و هنگامی که به لبهها میرسند جهت حرکت را معکوس و حرکت خود را پیدرپی تکرار میکنند. اگر اسکیتبازها در خارج از فاز حرکت کنند، -یکی به لبه برسد، درحالی که دیگری در حال گذر از مرکز است- نسبت به حالتی که داخل فاز هستند، -هر دو در یک لحظه در حال گذر از مرکز هستند- رقصآرایی بالاتری خواهند داشت. در حالت اول، حرکتها دارای تقارن کامل مربعی هستند، زیرا مجموعه یکسانی از چرخشها و بازگشتها در طول زمان، موجب میشود که کل سیستم بدون تغییر بماند. حالت دوم تقارن پایینتری دارد. بویل میگوید به طور کلی انواع زیادی از کریستالهای رقصان وجود دارد، اما تنها تعداد اندکی از آنها دارای رقصآرایی بسیار بالا هستند.
بویل اظهار امیدواری کرد که کریستالهای رقصان با بسیاری از مسائل ریاضی جور درآید، زیرا نظریه ثابت شبکههای استاندارد رقصان کاربردهای زیادی یافتهاند، از نظریه اعداد بدون دیمانسیون (بُعد) تا تصحیح خطا در محاسبات. پژوهشگران اذعان کردند که نمیتوانند بگویند آیا این کریستالها به طور طبیعی وجود خواهند داشت یا خیر، با وجود اینکه فکر میکنند حرکت هستهها و الکترونهای اتم در جامدات میتواند به این شکل هماهنگ شود. اگر چنین باشد، شناسایی رقصآراییها با استفاده از روشهای پراش، همانند روشی که در بلورشناسی به کار میرود، امکانپذیر خواهد شد –وجود رقصآرایی موجب میشود علامت مشخصه متمایزی به طرح پراش اضافه شود. کریستالهای رقصان را میتوان به صورت دلخواه و مصنوعی ساخت، پژوهشگران ادعا میکنند برای مثال میتوان این کار را با به دام انداختن اتمها و ذرات در دامهای الکترومغناطیسی، که توسط میدانهای نوری شدید ایجاد میشود، انجام داد.
جیمز کراچفیلد، از متخصصین دینامیک پیچیده در دانشگاه کالیفرنیای دیویس میگوید: این پژوهش «زنجیرهای زیبا از نظریه گروه و دینامیکهای تناوبی» نام دارد. او هماکنون امیدوار است بتواند این روش را برای «کریستالهای» با نظم کمتر عمومیسازی کند، یعنی همان کاری را که بویل و همکارانش برای کریستالهای رقصان انجام دادند.
این پژوهش در Physical Review Letters منتشر شده است.
نویسنده: فیلیپ بال نویسنده مستقل علمی در لندن است و «جذبه پرخطر نادیدهها» (دانشگاه شیکاگو، 2015) نوشته اوست.
منبع: New Crystal Type is Always in Motion
مرجع: Symmetric Satellite Swarms and Choreographic Crystals
نویسنده خبر: مهسا توکلی دوست
آمار بازدید: ۳۲۰
ارجاع دقیق و مناسب به خبرنامهی انجمن بلا مانع است.»
 RSS
RSS