نظریه‌ی توییستورها بازنویسیِ نظریه‌ی برهم‌کنشِ میانِ ذرات است، یعنی همان نظریه‌ی استانداردِ شناخته‌شده هم‌اینک در قالبی تازه ارایه شده که بر پایه‌ی هندسه‌ی توییستوری بنا نهاده شده است. گمان می‌رود که این نظریه کاربردهای بسیاری در فیزیک، از جمله در بازفرمول‌بندیِ نظریه‌ی گرانش داشته باشد.

اخبارِ مربوط به پیش‌رفت‌ها در فیزیکِ بنیادی بر گزارشِ یافته‌هایی متمرکز شده که از نظریه‌های پذیرفته‌شده تا به امروز، پا فراتر می‌نهند و یا حتی آن‌ها را سرنگون می‌کنند. مسئله‌ی ماده‌ی تاریک نمونه‌ای از این دست است که از تلاش برای سازگار کردنِ توزیعِ قابلِ مشاهده‌ی جرمِ کهکشان‌ها با مدلِ استانداردِ ذراتِ بنیادی به وجود آمد و نشان داد هنوز چیزهای شگفتِ بسیاری برای آموختن وجود دارد. اما داستان تنها این نیست. توصیفی نوین و انقلابی از آن‌چه پیش‌تر پایه‌گذاری شده نیز به اندازه‌ی ارایه‌ی نظریه‌های جدید، اهمیت دارد.

پایانِ دهه‌ای سرشار از چنین پیش‌رفت‌هایی به ما نشان می‌دهد که روش‌های به کار گرفته شده از سال‌های 1940 به این سو، هم‌اینک به چالش کشیده شده‌اند. نظریه‌ها نادرست نیستند، بلکه فرمول‌بندیِ دوباره‌ی آن‌ها بسیار سودمند خواهد بود. نگاهی کوتاه به نسخه‌ی پیش‌ازچاپِ مقاله‌ای [1] که توسطِ گروهی به سرپرستیِ نیما ارکانی‌حامد (Nima Arkani-Hamed) نوشته شده، جلوه‌ای نو و ناآشنا از برهم‌کنشِ میانِ ذرات را به نمایش می‌گذارد. عنوانِ این مقاله «دامنه‌های پراکندگی و گراسمانیِ مثبت» است. تصویری که در زیر آورده شده شبکه‌هایی را نشان می‌دهد که به کمکِ پایانه‌های رنگی، راس‌های روشن و تیره را به یک‌دیگر پیوند می‌دهد. این تصویر که به مقاله‌ی 154 صفحه‌ایِ ارکانی‌حامد [1] پیوست شده، بیش‌تر به اثری هنری از گالریِ (هنرهای) مدرنِ تِیت (Tate Modern gallery) می‌ماند (آلن تِیت شاعری آمریکایی‌ست که این گالری به نامِ وی نام‌گذاری شده است). اما آن‌چه که این تصاویر واقعاً نشان می‌دهند از این هم شگفت‌انگیزتر است: این تصاویر انتشارگرها را در «فضای توییستوری» نشان می‌دهد. در واقع فضای توییستوری مفهومی‌ست که تنها شمارِ بسیار اندکی از فیزیک‌دانان با آن آشنا هستند.

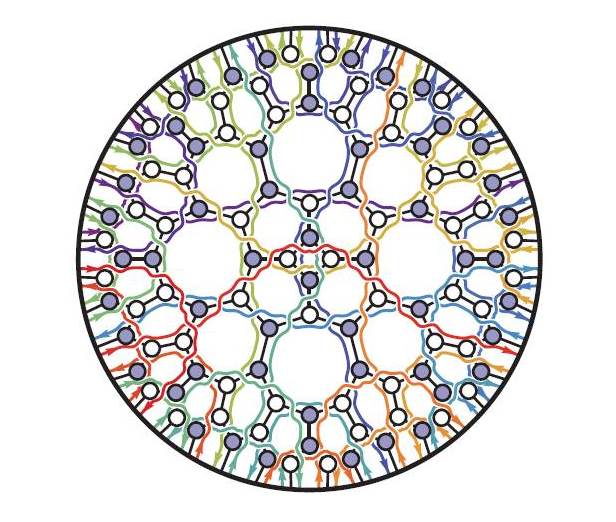
اما این تصاویر بر پایه‌ی گمانه‌زنی به دست نیامده‌اند، بلکه مبنای عملی دارند. آزمایش‌هایی که شاملِ برخوردِ ذرات به یک‌دیگر هستند یک مشکلِ عملیِ عمده دارند: برای آن‌که بتوانیم چیزی نو و غیرِ منتظره بیابیم باید توصیفی موثر و قابلِ اعتماد از پیش‌بینی‌ها و دانسته‌های قدیمی‌تر داشته باشیم. اگرچه «پس‌زمینه‌ای» که در اثرِ برخوردِ ذرات به یک‌دیگر ایجاد می‌شود را می‌توان به کمکِ مدلِ استانداردِ (ذراتِ بنیادی) پیش‌بینی کرد، اما این پس‌زمینه هنوز به اندازه‌ای پیچیده است که انجامِ محاسبات در موردِ آن بسیار دشوار می‌نماید. در اصل، نظریه‌ی مربوط به برخوردِ ذرات در سال‌های پایانی دهه‌ی 1940 حل شده بود و از آن روز، نسل‌هایی از فیزیک‌دانان در پیِ هم آمده‌اند تا ببینند نمودارهای ریچارد فاینمن (Richard Feynman) چه چیزی برای گفتن دارند. وی دراین نمودارها به کمکِ برهم‌کنش‌های میانجی میانِ ذراتِ «مجازی»، تصویری از واقعیت را پدیدار می‌کند. اما باید توجه کرد که ذراتِ مجازیِ فاینمن موجوداتی کاملاً ریاضی هستند و نمی‌توان آن‌ها را به طورِ مستقیم مشاهده کرد. افزون بر این ریاضیات، سرشتی غیرِ تجربی دارد و این موضوع در زمینه‌ی بررسیِ کوارک‌ها و گلوئون‌هایی که در رخ‌دادهای زیرهسته‌ای به وجود می‌آیند ایجاد مشکل می‌کند. باید سهمِ مربوط به میلیون‌ها نمودارِ (فاینمن) را با یک‌دیگر جمع بست تا بتوان به توصیفِ فیزیکیِ معناداری رسید. از دهه‌ی 1980 آشکار شد که پاسخ‌هایی که (از روشِ نموادارهای فاینمن) به دست می‌آیند بسیار ساده‌تر از خود ِراه‌کارها و روش‌هایی هستند که به کار گرفته می‌شوند. به همین دلیل روش‌های نوینی پدید آمدند که همان نتایج به کمکِ آن‌ها به صورتِ سرراست‌تری به دست می‌آمد.

یکی از واژه‌هایی که برای توصیفِ این روش‌های نوین به‌کار می‌رود «روی پوسته» است. این نام‌گذاری به این معناست که این روش‌ها تنها با هندسه‌ی میدان‌های واقعی سروکار دارد و نه میدان‌های مجازی. «دَستیدِگی» و «اسپینورها» واژگانِ سرنوشت‌سازِ دیگری هستند که در واقع، حالت‌هایی با دستیدگیِ خالص را معرفی می‌کنند. اسپینورها که به مانندِ جذرِ بردارها می‌مانند موجوداتِ تازه و ناشناخته‌ای نیستند و ریاضیاتِ مربوط به آن‌ها به قرنِ نوزدهم باز می‌گردد. هنگامی که دیراک (Dirac) معادله‌ی خود را برای توصیفِ الکترون ارایه کرد، این موجودات (اسپینورها) نقشِ عمده‌ای در مکانیکِ کوانتومی یافتند. دیراک سخت تلاش می‌کرد که الکترون به صورتِ موجودی یکتا توصیف شود اما از دورنمای مدلِ استانداردِ نوین می‌دانیم که (تابعِ موجِ) الکترون به طورِ طبیعی به دو بخشِ راست‌دست و چپ‌دست تجزیه می‌شود. اسپینورهایی که این دو بخش را توصیف می‌کنند ساده‌تر هستند و در واقع همین توصیفِ اسپینوری‌ست که ره‌یافتِ نوین به نظریه‌ی پراکندگی را به صورتِ اساسی، ساده‌تر کرده است.

توییستورها که در سال‌های دهه‌ی 1960 توسطِ راجر پن‌رز (Roger Penrose) معرفی شد در واقع هندسه‌ی اسپینوری را به تصویرِ نوینی از فضازمان گسترش داد. یعنی همان‌گونه که اسپینورها هم‌چون جذرِ بردارها و یا به عبارتِ دیگر، جذرِ راستاها هستند، توییستورها به گونه‌ای جذری از خودِ فضازمان هستند. در سالِ 1972 پن‌رز نخستین نمودارِ توییستوری برای پراکندگیِ ذرات را نوشته و محاسبه کرد [2]. این نمودار شاملِ همان رئوسِ تیره و روشنی بود که هم‌اینک در این کارِ تازه نیز به چشم می‌خورد [1]. این رئوسِ تیره و روشن در واقع بیان‌گرِ دوگانیِ راست‌دستی و چپ‌دستی در تابعِ موجِ الکترون است.

این سفر سال‌ها به طول انجامید. این مباحث در سالِ 2003 به یک‌دیگر پیوند خورد، هنگامی که اِد ویتن (Ed Witten) دیدگاه‌هایی از نظریه‌ی ریسمان، دانسته‌هایی از هندسه‌ی توییستوری و نیازهای عملی برای انجامِ محاسباتِ مربوط به پراکندگی را گردِ هم آورد [3]. به کمکِ همین پژوهش‌ها بود که نمودارهای توییستوریِ پن‌رز انگیزه‌ای برای نوزایی یافت. در سالِ 2005 من (Andrew Hodges) نشان دادم که چگونه این نمودارها در دلِ نظریه‌ی تازه‌ی ویتن، جای می‌گیرند. سپس بر اساسِ همین محاسبات، ارکانی‌حامد و هم‌کارانش [4] در سالِ 2009 حسابِ نوینی برای نظریه‌ی پراکندگی آفریدند که مفهومِ هندسی و کلاسیکی از «گراسمانی» در آن نقشِ اصلی را بازی می‌کرد. فضای گراسمانی فضایی‌ست که همه‌ی زیرفضاهای خطیِ یک فضای برداری را پارامتربندی می‌کند. (ارکانی‌حامد و ویتن در سالِ گذشته به طورِ جداگانه جایزه‌ی فیزیکِ بنیادی به مبلغ سه ملیون دلارِ آمریکا را از آنِ خود کردند).

هم‌اینک گروهِ پژوهشیِ ارکانی‌حامد این دیدگاه را گسترش داده و تصویری بسیار کامل‌تر از آن ارایه داده‌اند. یکی از ویژگی‌های چشم‌گیرِ این دیدگاه، پیوندِ زیبایی‌ست که با ریاضیاتِ محض دارد، ریاضیاتی که هندسه‌دانان تا به امروز به دلایلِ کاملاً متفاوتی آن را پی‌گیری می‌کرده‌اند. وجودِ مفهومِ «گراسمانیِ مثبت» به این معناست که این دیدگاه پیوندِ سرراستی با ساختارِ ساده‌ی جای‌گشت‌ها دارد.

چهل سال پیش، پن‌رز نه تنها امیدوار بود که هندسه‌ی توییستوری توصیفِ بهتری از نظریه‌های پذیرفته شده به دست دهد بلکه می‌پنداشت که چنین دگرگونیِ انقلابی در الگوها، تولدِ نظریه‌های فیزیکیِ کاملاً نوینی را سبب خواهد شد. نمونه‌ای تاریخی که همانندی‌های تقریبی با این موضوع دارد هندسه‌ی چهاربعدیِ اینشتین و مینکوفسکی‌ست که در ابتدا تنها توصیفِ ساده‌تر و کامل‌تری از نظریه‌ی الکترومغناطیسِ کلاسیکِ ماکسول به دست می‌داد، اما درواقع ایجادِ تصویری نوین از ذراتِ بنیادی و نیروها را ممکن ساخت، نقشی که شاید در سالِ 1900 غیرِ قابلِ تصور بود. همان‌گونه که پن‌رز در سالِ 1972 اشاره کرد نظریه‌ی توییستور بر آن است که همه‌چیز، از جمله گرانش و پیوندِ آن با جرم را دگرگون سازد.

پیش‌رفت‌های تازه‌ای نیز به دست آمده است. نسخه‌ی پیش‌ازچاپِ مقاله‌ای از دیوید اسکینر (David Skinner) منتشر شده که در آن زنجیره‌ای طولانی از ایده‌ها و یافته‌ها آورده شده و کارِ پژوهشیِ ویتن در سالِ 2004 را چنان سازگار می‌کند که ابزارِ عملیِ نوینی برای محاسبه‌ی دامنه‌ی پراکندگی‌های گرانشی به دست می‌دهد. محاسبه‌ی دامنه‌ی پراکندگیِ گرانشی به کمکِ نظریه‌ی استاندارد، حتی از محاسبه‌ی دامنه‌ی پراکندگیِ ذراتِ زیرهسته‌ای و نیروها نیز دشوارتر است. این دیدگاه، نظریه‌ی تازه‌ای برای گرانش نیست بلکه صورتِ کاملاً نوینی از همان نظریه‌ی استاندرد است که ایده‌ای نوپا دارد: اگر نظریه شاملِ ثابتِ کیهان‌شناختی (یا «ماده‌ی تاریک») باشد و از این ایده دست برداریم که فضازمانِ تختِ مینکوفسکی را به عنوانِ پس‌زمینه در نظر بگیریم، نظریه‌ی گرانش بسیار ساده‌تر خواهد شد. به دلیلِ روشی که به کمکِ آن می‌توان از میانِ رصدهای مربوط به کیهانِ نخستین، این دیدگاه را دریافت، علاقه‌ی زیادی به هندسه‌ی (توییستوری) وجود دارد. اما این اندیشه که هندسه‌ی توییستوری ممکن است نقشی اساسی در توصیفِ دامنه‌های پراکندگی بازی کند، ایده‌ای تازه است. ثابتِ کیهان‌شناختی بیانِ زیبا و گیرایی در هندسه‌ی توییستوری دارد، دیدگاهی که حالا ممکن است توجه‌های بیش‌تری به خود جلب کند.

منبع

http://www.nature.com/nphys/journal/v9/n4/full/nphys2597.html

مرجع‌ها

1. Arkani-Hamed, N. et al. Preprint at http://arxiv.org/

1212.5605 (2012).

2. Penrose, R. & MacCallum, M. A. H. Phys. Rep. 6, 241–316 (1972).

3. Witten, E. Commun. Math. Phys. 252, 189–258 (2004).

4. Arkani-Hamed, N., Cachazo, F., Cheung, C. & Kaplan, J. J. High Energy Phys. 1003, 020 (2010).

5. Skinner, D. Preprint at http://arxiv.org/1301.0868 (2013).