- جایزه انجمن فیزیک ایران
- جایزه حسابی
- جایزه دبیر برگزیده فیزیک
- جایزه ساخت دستگاه آموزشی
- جایزه صمیمی
- جایزه توسلی
- جایزه علی محمدی
- پیشکسوت فیزیک
- بخش جوایز انجمن
این ایده که کل یک سامانه میتواند چیزی بیشتر از مجموع زير-قسمتهایش داشتهباشد، اهمیت زيادي در دانش دارد: رفتار چنین سامانهی ترکیبی را نمیتوان به سادهگی از بررسی بخشهای آن بهدست آورد. این پدیده، در دانشهای کوانتومی، به شکلی خاص ظاهر میشود: در هر سامانهی کوانتومی، کمیتهای فیزیکی خاصی، مطابق با نوع آن سامانه، جمعپذیر نخواهندبود [۱]. اگر کلیگویی کنیم، چیزی مانند 0+0>0 یا کره گرفتن از آب است. سرچشمهی این اثر در این حقیقت نهفته است که مکانیک کوانتومی اجازه میدهد دو سامانه (یا بیشتر) در ارتباط با هم اندازهگیری شوند؛ و این همتای کلاسیکی ندارد. کارلوس پالازوئلوس از موسسهی دانشهای ریاضی در اسپانیا در Physical Review Letters تصویری ویژه از این پدیده ارائه میدهد: غیرموضعی بودن، یکی از غیرشهودیترین شاخصههای نظریهی کوانتومی، جمعپذیر نمیباشد: ترکیب شماری از حالتهای کوانتومی موضعی میتواند غیرموضعی باشد.
S. Massar and S. Pironio, Physics 5, 56 2012
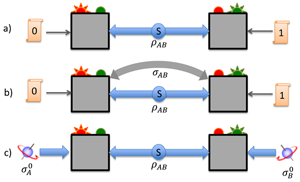
شکل۱ حالتهای کوانتومی درهمتافتهی موضعی ترکیب شده و یک حالت کوانتومی غیرموضعی میدهند. الف) چشمهی S دو بخش از یک حالت کوانتومی ρ را به دو مشاهدهگر میفرستد. حالت ρ موضعیست: آمار همبستهگی اندازهگیریشده بهدست مشاهدهگرها را نمیتوان از مورد کلاسیکی تشخیص داد چراکه نابرابری بل را نقض نمیکنند. این حالت غیرموضعی نیست. ب) یک حالت غیرموضعی میتواند از ترکیب شماری از نسخههای ρ بهدست آید. پالازوئلوس نشان میدهد که آمار همبستهگی مشاهدهشده برای حالت ترکیبی میتواند نابرابری بل را نقض کند؛ یعنی این حالت غیرموضعیست. بهطورکلی، در مکانیک کوانتومی صفر به اضافهی صفر میتواند بیشتر از صفر شود.
موضعی بودن یعنی اینکه جسم تنها تاثیر مستقیم محیط نزدکش را میبیند و نه اجسامی در فاصلهی دور. این حقیقت که مکانیک کوانتومی با این اصل تناقض دارد، تازه نیست. اولینبار، آنستاین، پودولسکی، روزن و شرودینگر در، دههی ۳۰، با مطرح کردن امکان درهمتافتهگی کوانتومی، این جنبهی چشمگیر نظریهی کوانتومی را زیر سوال بردند؛ و این بدانجا رفت که اندیشیدند که یک جای کار مکانیک کوانتومی میلنگد و گامهای بعدی در پیشبرد نظریه باید در سویی برداشته شود که اصل موضعیبودن احیا شود. اما سالها بعد این امید با [خطای پردازش ریاضی] و با کار بل که در آن گفته شد مکانیک کوانتومی ذاتا غیرموضعی و با هر اصلی که بنابر موضعی بودن باشد در تناقض است، نقش بر آب شد [۲]. بل اینگونه بحث کرد که در هر نظریهی موضعی حدی روی فاصلهای که در آن رویدادها همبستهاند، وجود دارد؛ و از نظر ریاضی، آمار همبستهگی باید نابرابریهای خاصی را دنبال کند. بل نشان داد که دو مشاهدهگر که حالتهای درهمتافته را اندازهگیری میکنند، ممکن است همبستهگی بالایی میان نتیجهها ببینند: چنین همبستهگیهایی میتوانند آنچنان قوی باشند که نابرابری بل را نقض کنند.
این پدیده که غیرموضعیبودن کوانتومی خوانده میشود، در آزمایشها بسیاری مشاهده میشود؛ مانند آزمایشهای نورشناسی کوانتومی، که درستکردن فوتونهای درهمتافتهی قطبشی در آنها بسیار فراوان شدهاست. سپس هرکدام از فوتونهای یک جفت (مثلا با یک فیبر نوری) به مشاهدهگری که میتواند قطبش را بررسی کند و در مسافتی دور است، فرستاده میشوند. همبستهگی مشاهدهشده میان نتیجهی اندازهگیریها، میتواند به نقض نامساوی بل بیانجامد و شاهدی باشد بر اینکه دنیای فیزیکی غیرموضعیست [۳]. ابتدا درهمتافتهگی و غیرموضعیبودن را دو نمود از یک اثر فیزیکی میدانستند؛ اما همانطور که در این گروه نشان داده شدهاست، درواقع دو ویژگی متفاوتاند [۴]. بههرروی، رابطهی میان آنها باید کاملا فهمیدهشود. در حالیکه درهمتافتهگی برای غیرموضعیبودن لازم است، کافی نمیباشد. در نتیجه، حالتهای درهمتافتهای که همچنان موضعیاند، وجود دارند: از آنجا که حالتهای کوانتومی درهمتافته، نامساوی بل را نقض نمیکنند، میتوان با روشی بدانها دستیافت که آمار همبستهگیشان را نیز نتوان از مورد کلاسیکی تشخیص داد [۵].
در ترکیب چند حالت درهمتافتهی موضعی چه رخ میدهد؟ آیا غیرموضعیبودن حالت کلی (ترکیبی) تنها نتیجهی غیرموضعیبودن حالتهای ابتدایی است؟ به بیانی دیگر، غیرموضعیبودن جمعپذیر است، یا اثرهای ظریفتری رخ میدهند؟ این پرسش، فراتر از جنبههای انتزاعی، با دانش دادههای کوانتومی که در آن غیرموضعیبودن کلید پردازش است، مرتبط میباشد. مانند روشهای کوانتومی رمزنگاری ایمن که بر غیرموضعیبودن تکیه دارند: همبستهگی قوی کوانتومی میان بیتهایی که بخشهای ارتباطی ردوبدل میکنند، میتواند یک کلید رمزگشایی سری به دست دهد که تنها خود آنها بدان آگاه خواهند بود[۶]. در نتیجه اگر یکیشان با ترکیب دو حالت موضعی (و درنتیجه از نظر رمزنگاری بیفایده)، به حالتی غیرموضعی دستیابد، چشمانداز تازهای گشوده میشود.
در سالهای اخیر، شماری از پژوهشگران [۷] کوشیدهاند که جمعپذیری غیرموضعیبودن کوانتومی را به چالش کشند. در این کار، پالازوئلوس یک اثبات محض ارائه میدهد که غیرموضعیبودن کوانتومی جمعپذیر نیست: هستند حالتهای درهمتافتهی موضعی که نتیجهی ترکیب چند نسخه از آنها غیرموضعی میشود. نویسنده با یک حالت کوانتومی خاص که درهمتافته ولی موضعیست ([خطای پردازش ریاضی])، آغاز میکند؛ سپس نشان میدهد که چهگونه میتوان با ترکیب چند نسخه از [خطای پردازش ریاضی] یک حالت غیرموضعی ساخت ([خطای پردازش ریاضی] ⊗ [خطای پردازش ریاضی] ⊗ [خطای پردازش ریاضی] ⊗...⊗ [خطای پردازش ریاضی]). نشان دادهمیشود که اگر شمار بالایی از نسخهها ترکیب شوند، حالت کلی از نابرابری بل تخطی میکند؛ یعنی اینکه غیرموضعیست (شکل ۱ را ببینید). این فرآیند را در نمونهی زیر میتوان دید. چشمهای را در نظر آورید که جفتفوتونهای درهمتافتهی قطبشی [خطای پردازش ریاضی] گسیل میدارد که با دو مشاهدهگر شناسایی میشوند. این حالت باید موضعی باشد: همبستهگی اندازهگیری شده به دست مشاهدهگرها آنقدر قوی نیستند که غیرموضعیبودن بهبارآورند. و هر مشاهدهگر میتواند اندازهگیریهای همزمانی بر فوتونهای [خطای پردازش ریاضی]ی که دریافت میکند، انجام دهد؛ و نابرابری بل نقض خواهد شد. بنابراین حالت کلی که دربردارندهی نسخههایی از [خطای پردازش ریاضی] است، غیرموضعی خواهد بود.
از آن روی که مکانیک کوانتومی «اندازهگیریهای درهمتافته» را که همتای کلاسیکی ندارند، ممکن میسازد، این اثر دیده میشود. میتوان دو سامانهی کوانتومی (یا بیشتر) را بههموابسته و در پایههای درهمتافته بررسی کرد (یعنی پایههایی که در آنها ویژهکتها در همتافتهاند). به بیانی کلی؛ میتوان اندازهگیریهای بههموابستهای در راستای استخراج دادههایی دربارهی حالت کلی سامانه، بدون آشکار ساختن ویژهگیهای جداگانه، در نظر آورد. به عنوان نمونه، همین را در بررسی درهمتافتهگی قطبشی دو فوتون میبینیم که بدون آشکارسازی قطبش تکتک فوتونها، به ما میگوید که آیا یکساناند یا خیر. چنین اندازهگیریهایی که در دورنوردی و کامپیوترهای کوانتومی نقشی محوری دارند، کلید یافتههای پالازئوس نیز هستند.
یک بخش کلیدی دیگر در اثبات پالازوئلوس وجود طبقهای از نقضهای نابرابری بل است که اتفاقا خود او و همکارانش کشفشان کردهاند و «غیرمقیدها» خواندهمیشوند. آنها اثباتی ریاضی ارائه دادهاند که بنابرآن میتوان به حالتهای کوانتومی خاصی رسید که همبستهگیهایشان به شدت قویتر از همبستهگیهای دیدهشده در شرایط کلاسیکیاند. در واقع، با یک انتخاب خوب برای حالتها و اندازهگیریها، میشود که جدایی کوانتومی نسبت به مورد کلاسیکی به طور دلخواهی بزرگ، و آنگونه که گفتیم «غیرمقید» شود. مرجع [۸] اثبات وجودی ریاضی را در بردارد؛ بوهرمن و همکاران اولین نمونهی حالت کوانتومی [خطای پردازش ریاضی] را که در آن نابرابری بل به روش غیرمقیدها نقض میشود، گزارش کردهاند. با داشتن این دانش، پالازئولس گام بعدی را برداشت؛ حالت کوانتومی که بوهرمن و همکاران گزارش دادهاند، میتواند شکل سادهای داشتهباشد: میتوان آن را به این صورت شکست که [خطای پردازش ریاضی] = [خطای پردازش ریاضی] ⊗ [خطای پردازش ریاضی] ⊗...⊗ [خطای پردازش ریاضی] (ضرب[خطای پردازش ریاضی]) که در آن [خطای پردازش ریاضی] یک حالت درهمتافتهموضعیست.برای [خطای پردازش ریاضی] ِ به اندازهی کافی بزرگ، نابرابری بل نقض میشود. این اثر بیشفعالی غیرموضعی کوانتومی خوانده میشود.
از آنجا که کارهای پالازئولوس یکی از قدیمیترین پرسشها دربارهی غیرموضعی بودن کوانتومی را حل کرده، میتواند نمایانگر رشدی باشد که در این زمینه بهدست آمدهاست. اما پرسشهای دیگری نیز پیش میآیند. یک پرسش مهم آن است که بیشفعالی غیرموضعی برای هر حالت درهمتافته که نمودی موضعی دارد، ممکن است؟ پیشرفتی در این جهت گزارش شدهاست: به تازهگی گروهی از پژوهشگران [۱۰] که یکی از اعضای همین گروه نیز با آنها همراه است (N.B.)، با بهکاربستن یافتههای پالازئوس، نشان دادهاند که تمام حالتهای درهمتافتهای که برای دورنوردی مفیدند، میتوانند دچار بیشفعالی شوند؛ و این پیوند محکمی میان دورنوردی و غیرموضعیبودن –که پیشتر باور بر این بود که با هم ارتباطی ندارند[۱۱]- ایجاد میکند. در بلندمدت، ممکن است این ایدهها به درک چهگونهگی ارتباط درهم تافتهگی و غیرموضعیبودن که پرسشی مهم در مکانیک کوانتومی و دانش دادههای کوانتومیست، بهره برساند.
منبع:
http://physics.aps.org/articles/v5/124
مرجع:
- C. Palazuelos, “Superactivation of Quantum Nonlocality,” Phys. Rev. Lett. 109, 190401 (2012).
- J. S. Bell, “On the Einstein Podolsky Rosen Paradox,” Physics 1, 195 (1964).
- A. Aspect, “Bell’s Inequality Test: More Ideal Than Ever,” Nature 398, 189 (1999).
- N. Brunner, N. Gisin, and V. Scarani, “Entanglement and Nonlocality are Different Resources,” New J. Phys. 7, 88 (2005).
- R. F. Werner, “Quantum States with Einstein-Podolsky-Rosen Correlations Admitting a Hidden-Variable Model,” Phys. Rev. A 40, 4277 (1989); M. L. Almeida, S. Pironio, J. Barrett, G. Toth, and A. Acin, “Noise Robustness of the Nonlocality of Entangled Quantum States,” Phys. Rev. Lett. 99, 040403 (2007).
- A. K. Ekert, ”Quantum Cryptography Based on Bell’s Theorem,” Phys. Rev. Lett. 67, 661 (1991); J. Barrett, L. Hardy, and A. Kent, “No Signaling and Quantum Key Distribution,” 95, 010503 (2005); A. Acin, N. Gisin, and L. Masanes, ”From Bell’s Theorem to Secure Quantum Key Distribution,” Phys. Rev. Lett. 97, 120405 (2006).
- L. Masanes, Y.-C. Liang, and A. C. Doherty, “All Bipartite Entangled States Display Some Hidden Nonlocality,” Phys. Rev. Lett. 100, 090403 (2008); D. Cavalcanti, M. L. Almeida, V. Scarani, and A. Acin, “Quantum Networks Reveal Quantum Nonlocality,” Nat. Comm. 2, 184 (2011); A. Sen(De), U. Sen, Č. Brukner, V. Bužek, and M. Żukowski, “Entanglement Swapping of noisy states: A kind of superadditivity in nonclassicality,” Phys. Rev. A 72, 042310 (2005).
- M. Junge, C. Palazuelos, D. P´erez-Garcia, I. Villanueva, and M. M. Wolf, “Operator Space Theory: A Natural Framework for Bell Inequalities,” Phys. Rev. Lett. 104, 170405 (2010).
- H. Buhrman, O. Regev, G. Scarpa, , and R. de Wolf, “Near-Optimal and Explicit Bell Inequality Violations,” IEEE Conference on Computational Complexity 2011, 157 (2011).
- D. Cavalcanti, A. Acin, N. Brunner, and T. Vertesi, “All Quantum States Useful for Teleportation are Nonlocal Resources,” arXiv:1207.5485.
- S. Popescu, “Bell’s Inequalities Versus Teleportation: What is Nonlocality?” Phys. Rev. Lett. 72, 797 (1994).
نویسنده خبر: سعیده هوشمندی
آمار بازدید: ۳۳۰
ارجاع دقیق و مناسب به خبرنامهی انجمن بلا مانع است.»
 RSS
RSS