انجمن @ شبکههای اجتماعی

جوایز انجمن
- جایزه انجمن فیزیک ایران
- جایزه حسابی
- جایزه دبیر برگزیده فیزیک
- جایزه ساخت دستگاه آموزشی
- جایزه صمیمی
- جایزه توسلی
- جایزه علی محمدی
- پیشکسوت فیزیک
- بخش جوایز انجمن
آخرین خبرها
«استفاده از اخبار انجمن فیزیک ایران و انتشار آنها، به شرط
ارجاع دقیق و مناسب به خبرنامهی انجمن بلا مانع است.»
شرح خبر
اخبار علمی و پژوهشی
زلزلههای کوچک در آزمایشگاه (۱۳۹۱/۱۲/۱۸)
آزمایشهایی که در مقیاس آزمایشگاهی انجام شده حاکی از شباهت آماریِ قابل ملاحظهای بین شکستگیِ مواد ناهمگن و زمینلرزهها است.
دههی ۱۹۷۰ دههای بود که در آن تحقیقات زلزلهشناسی با درجهی بالایی از خوشبینی به پیش میرفت و گمان میرفت که به زمان پیشگویی زلزله نزدیک شدهایم. این نگاه٬ از فرضی نشات میگرفت که در آن لرزههای ایجاد شده در زمینلرزه با آنچه در آزمایشگاه بر روی شکستگی نمونههایی از سنگ رخ میداد٬ شباهت نزدیکی فرض شده بود [1]. چنین انتظاراتی به این عقیده منجر شد که پیشنشانگرهای تشخیصیِ زلزله (همچون پدیدههای الکترومغناطیسی یا صوتی و غیره) را میتوان شناسایی کرد. اما این خوشبینی اولیه بهعنوان نشانگرهای قابل اعتماد وقتی تحت آزمایشاتِ آماری [2]٬ و نیز نتایج نظریات موهومی [3] قرار گرفت٬ دچار تزلزل شد و توضیحِ فیزیکیِ را برای غیاب چنان نشانگرهایی فراهم ساخت.
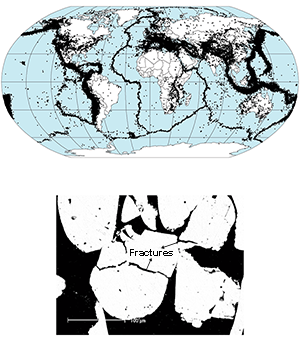
هرچند پیشگویی و تعیین تکتکِ زمینلرزهها با دقت کافی هنوز دور از دسترس است و حتی شاید یک هدف علمیِ واقعی هم به حساب نیاید [5]٬ اما پیشبینی احتمالی زلزله هنوز در حال پیگیریاست. چون این حوادث اتفاقی نبوده و عمدتاً بر روی صفحات مرزی جایگزیده شدهاند (شکل ۱ را ببینید) و در طول زمان به سمت رفتار خوشهای تمایل دارند[6].
آمار زمینلرزهها از محدودهای از قوانین مقیاسی تجربی تبعیت میکنند. چنین قوانینی محدودیتهای شدیدی بر فیزیکِ رویدادِ زلزلهها اعمال میکنند. مدلهای زلزله معمولاً با استفاده از قوانین ترکیبی که از آزمایشهای شکستگی و اصطکاک٬ که در آزمایشگاه انجام میشود٬ ساخته میشوند. اما نکته در اینجاست که مقایسههای دقیق آماری بین چنین آزمایشهایی و زمینلرزههای واقعی وجود نداشت.
بر اساس مقالهای که جوردی بارو (Jordi Barò) از دانشگاه بارسلونا در اسپانیا و همکارانش در مجلهی فیزیکال ریویو لیترز ارائه دادهاند٬ میتوان به مقایسههای آماری جامعی بین رویدادهای لرزهای در آزمایشگاه و طبیعت دست یافت [7]. آنها نشان دادند که در گسترهای از مراتب مختلفِ اندازه٬ دادههایی که از آزمایشهای انجام شده در آزمایشگاه بدست آمده و نیز دادههای پایگاهدادهی زمینلرزههای حادث شده٬ همگی در توزیع یکسانی متفق میشوند که نشان از قوانین مقیاسبندیِ بسیار مشابه میدهند.
چنین خوشهبندیِ توزیع احتمالیِ زمینلرزه در مکان و زمان٬ ناشی از پاسخ حساسی است که به افتوخیزهای کوچک در تنشهای محلی داده میشود و با سیستم فیزیکی که به حالت بحرانی نزدیک است سازگار است. منظور از این سیستم بحرانی یعنی اینکه شکست عنصری از سیستم میتواند باعث شکست عنصر دیگری شود که از لحاظ زمانی و مکانی به آن نزدیک است؛ مشابه سرایت یک بیماری واگیردار بین جمعیت محلی یک منطقه. براین اساس٬ آمارگران مدلِ زمینلرزهی احتمالاتیِ خالصی را توسعه دادند که دنبالهی پسلرزهایِ از نوعِ واگیر (epidemic-type aftershock sequence) نام دارد (ETAS).
سه قانون مقیاسبندی با اعتبار بسیار تعمیمیافتهتری به اثبات رسیدهاند. اولین آنها قانون گوتنبرگ-ریشتر (Gutenberg-Richter) است که بر این حقیقت استوار است که زمینلرزههای کوچک بسیار رایجتر از زمینلرزههای بزرگ هستند. دومین قانون٬ قانون اموری (Omori) است که چگونگیِ کاهش احتمال پسلرزهها را نسبت به زمان توصیف میکند. سرانجام آخرین قانون٬ معروف به «بهرهوریِ پسلرزه» نام دارد که آهنگ پسلرزههایی که توسط لرزهی اصلی ایجاد میشود را به اندازهی آنها ارتباط میدهد. مدلِ ETAS این سه قانون را با جمعیت تصادفیِ رویدادهای «زمینه»ی مستقلی٬ که باعث به راه انداختن دنبالهای از رویدادهای مشابه میشود٬ ترکیب کردهاند. یکی از نشانههای مهم چنین دنبالهای «نوفهی شکستگی» است: نوعی نوفه که از ترکیب رویدادهای شکستگیِ اتفاقی با خوشههای رویدادهای متناوب ناشی میشود؛ چیزی که وقتی کنار آتش نشستهایم یا هنگام خرد کردن کاغذ، به گوش میرسد. نوفهی شکستگی هم در زمینلرزه و هم تشکیل شکستگیهای کوچک در آزمایشگاه که بر روی شکستگی محیطهای دانهای یا ترکیبی به اثبات رسیده است.
بارو و همکارانش با استفاده از چارچوبِ مدلسازی ETAS، کار آزمایشگاهیِ جدیدی که بر روی آزمایش فشردگی در محیطِ دانهای انجام شده را با تحلیل کاتالوگِ زمینلرزهها (شامل جداولی از زمان٬ اندازه و موقعیت زمینلرزهها) مقایسه کردهاند. این آزمایشها شامل قرار دادن سرامیکِ سیلیسِ با تخلخل بالا در معرضِ فشردهسازیِ تکمحوری است که به شکل خطی تا زمانی افزایش مییابد که نمونهی مورد نظر به قطعات کوچک خرد شود. نتایج نشان از سازگاریِ قانون گوتنبرگ-ریشتر تا ۶-۷ مرتبه از بزرگیست. در زمان یکسان دادههای بدست آمده از آهنگهای فشردهسازی مختلف به یک تک منحنی فرو میریزند؛ که هم قانون اموری و هم قانون بهرهوری پسلرزهی مرتبط به آن را به دنبال دارد. نویسندگان این مقاله دریافتند که هر سه قانون مقیاسبندی در آزمایشهای آنان اعتبار دارد و تنها تفاوت جزئی در مولفههای مقیاسبندی نسبت به زمینلرزههای واقعی است.
کار دیگر این تیم عمق بخشیدن به تحلیلهایشان در مورد توزیع زمانهای انتظار بین رویدادهای متناوب بود. این تحلیلها تشابه قابل ملاحظهای با رفتار مقیاسبندی زمانهای انتظاری داشت که قبلاً توسط ETAS نسبت داده شده بود [9,10] و البته از مطالب اساسی جدیدی نیز برخوردار بود. به جای قانون توان اول با یک نوک نمایی (توزیعِ از نوع گاما) توزیعهای بدست آمدهی آنها با ترکیب قانون توان دوم سازگاری داشت. در نمودار دو-لگاریتمی (double-logarithmic) این موضوع به شکل توزیع پای-سگ (dog-leg) نمایان میشود: منحنی تشکیل شده از دو قطعه با شیبهای مختلف که شبیه پای عقبی یک سگ است. تحت شرایط پایا٬ مدلِ ETAS توزیع گامایی را تولید میکند که از ترکیب رویدادهای اتفاقی زمینه و پسلرزههای تصحیحیافته نتیجه میشود [9,10]. بارو و همکارنش نشان دادند که قانون پای-سگ به جای آن٬ ناشی از غیرپایایی موجود در آهنگ رویدادهای زمینه است. بحث آنها این بوده که منشاء ناپایایی در دو مورد متفاوت است. در آزمایشگاه این ناپایایی شتاب غیرخطی در آهنگ زمینه به عنوان یک تنش در زمان٬ افزایش می یابد و برای زمینلرزهها عمدتاً در اثر تغییرپذیری در آهنگ زمینهای است که به خوشهبندیِ مکانی مربوط است.
نتایج آزمایشها و کارهای تیمِ بارو نشان از این موضوع میدهد که مدلِ ETAS میتواند در تمامیِ مقیاسها از عهدهی مسائل مربوط به لرزهشناسی برآید. این مدل میتواند به توسعهی بهترِ پیشگوییهای احتمالی در مورد زمینلرزهها و دیگر مخاطرات همچون رانشِ زمین و آتشسوزیِ جنگلها نیز کمک شایانی کند. با این وجود تنها آزمایشهای گسترده با مشاهداتِ آینده است که از قدرت واقعی پیشبینیِ این رهیافت پرده برخواهد داشت و زمینه را برای هدایت آن بهسوی سیاستها و تصمیمات عملیاتی فراهم خواهد کرد.
دربارهی نویسنده:
ایان ماین (Ian Main) استاد لرزهشناسی و فیزیک سنگ در مدرسهی علومزمینی در دانشگاه ادینبرگ است.
مراجع:
دههی ۱۹۷۰ دههای بود که در آن تحقیقات زلزلهشناسی با درجهی بالایی از خوشبینی به پیش میرفت و گمان میرفت که به زمان پیشگویی زلزله نزدیک شدهایم. این نگاه٬ از فرضی نشات میگرفت که در آن لرزههای ایجاد شده در زمینلرزه با آنچه در آزمایشگاه بر روی شکستگی نمونههایی از سنگ رخ میداد٬ شباهت نزدیکی فرض شده بود [1]. چنین انتظاراتی به این عقیده منجر شد که پیشنشانگرهای تشخیصیِ زلزله (همچون پدیدههای الکترومغناطیسی یا صوتی و غیره) را میتوان شناسایی کرد. اما این خوشبینی اولیه بهعنوان نشانگرهای قابل اعتماد وقتی تحت آزمایشاتِ آماری [2]٬ و نیز نتایج نظریات موهومی [3] قرار گرفت٬ دچار تزلزل شد و توضیحِ فیزیکیِ را برای غیاب چنان نشانگرهایی فراهم ساخت.

هرچند پیشگویی و تعیین تکتکِ زمینلرزهها با دقت کافی هنوز دور از دسترس است و حتی شاید یک هدف علمیِ واقعی هم به حساب نیاید [5]٬ اما پیشبینی احتمالی زلزله هنوز در حال پیگیریاست. چون این حوادث اتفاقی نبوده و عمدتاً بر روی صفحات مرزی جایگزیده شدهاند (شکل ۱ را ببینید) و در طول زمان به سمت رفتار خوشهای تمایل دارند[6].
آمار زمینلرزهها از محدودهای از قوانین مقیاسی تجربی تبعیت میکنند. چنین قوانینی محدودیتهای شدیدی بر فیزیکِ رویدادِ زلزلهها اعمال میکنند. مدلهای زلزله معمولاً با استفاده از قوانین ترکیبی که از آزمایشهای شکستگی و اصطکاک٬ که در آزمایشگاه انجام میشود٬ ساخته میشوند. اما نکته در اینجاست که مقایسههای دقیق آماری بین چنین آزمایشهایی و زمینلرزههای واقعی وجود نداشت.
بر اساس مقالهای که جوردی بارو (Jordi Barò) از دانشگاه بارسلونا در اسپانیا و همکارانش در مجلهی فیزیکال ریویو لیترز ارائه دادهاند٬ میتوان به مقایسههای آماری جامعی بین رویدادهای لرزهای در آزمایشگاه و طبیعت دست یافت [7]. آنها نشان دادند که در گسترهای از مراتب مختلفِ اندازه٬ دادههایی که از آزمایشهای انجام شده در آزمایشگاه بدست آمده و نیز دادههای پایگاهدادهی زمینلرزههای حادث شده٬ همگی در توزیع یکسانی متفق میشوند که نشان از قوانین مقیاسبندیِ بسیار مشابه میدهند.
چنین خوشهبندیِ توزیع احتمالیِ زمینلرزه در مکان و زمان٬ ناشی از پاسخ حساسی است که به افتوخیزهای کوچک در تنشهای محلی داده میشود و با سیستم فیزیکی که به حالت بحرانی نزدیک است سازگار است. منظور از این سیستم بحرانی یعنی اینکه شکست عنصری از سیستم میتواند باعث شکست عنصر دیگری شود که از لحاظ زمانی و مکانی به آن نزدیک است؛ مشابه سرایت یک بیماری واگیردار بین جمعیت محلی یک منطقه. براین اساس٬ آمارگران مدلِ زمینلرزهی احتمالاتیِ خالصی را توسعه دادند که دنبالهی پسلرزهایِ از نوعِ واگیر (epidemic-type aftershock sequence) نام دارد (ETAS).
سه قانون مقیاسبندی با اعتبار بسیار تعمیمیافتهتری به اثبات رسیدهاند. اولین آنها قانون گوتنبرگ-ریشتر (Gutenberg-Richter) است که بر این حقیقت استوار است که زمینلرزههای کوچک بسیار رایجتر از زمینلرزههای بزرگ هستند. دومین قانون٬ قانون اموری (Omori) است که چگونگیِ کاهش احتمال پسلرزهها را نسبت به زمان توصیف میکند. سرانجام آخرین قانون٬ معروف به «بهرهوریِ پسلرزه» نام دارد که آهنگ پسلرزههایی که توسط لرزهی اصلی ایجاد میشود را به اندازهی آنها ارتباط میدهد. مدلِ ETAS این سه قانون را با جمعیت تصادفیِ رویدادهای «زمینه»ی مستقلی٬ که باعث به راه انداختن دنبالهای از رویدادهای مشابه میشود٬ ترکیب کردهاند. یکی از نشانههای مهم چنین دنبالهای «نوفهی شکستگی» است: نوعی نوفه که از ترکیب رویدادهای شکستگیِ اتفاقی با خوشههای رویدادهای متناوب ناشی میشود؛ چیزی که وقتی کنار آتش نشستهایم یا هنگام خرد کردن کاغذ، به گوش میرسد. نوفهی شکستگی هم در زمینلرزه و هم تشکیل شکستگیهای کوچک در آزمایشگاه که بر روی شکستگی محیطهای دانهای یا ترکیبی به اثبات رسیده است.
بارو و همکارانش با استفاده از چارچوبِ مدلسازی ETAS، کار آزمایشگاهیِ جدیدی که بر روی آزمایش فشردگی در محیطِ دانهای انجام شده را با تحلیل کاتالوگِ زمینلرزهها (شامل جداولی از زمان٬ اندازه و موقعیت زمینلرزهها) مقایسه کردهاند. این آزمایشها شامل قرار دادن سرامیکِ سیلیسِ با تخلخل بالا در معرضِ فشردهسازیِ تکمحوری است که به شکل خطی تا زمانی افزایش مییابد که نمونهی مورد نظر به قطعات کوچک خرد شود. نتایج نشان از سازگاریِ قانون گوتنبرگ-ریشتر تا ۶-۷ مرتبه از بزرگیست. در زمان یکسان دادههای بدست آمده از آهنگهای فشردهسازی مختلف به یک تک منحنی فرو میریزند؛ که هم قانون اموری و هم قانون بهرهوری پسلرزهی مرتبط به آن را به دنبال دارد. نویسندگان این مقاله دریافتند که هر سه قانون مقیاسبندی در آزمایشهای آنان اعتبار دارد و تنها تفاوت جزئی در مولفههای مقیاسبندی نسبت به زمینلرزههای واقعی است.
کار دیگر این تیم عمق بخشیدن به تحلیلهایشان در مورد توزیع زمانهای انتظار بین رویدادهای متناوب بود. این تحلیلها تشابه قابل ملاحظهای با رفتار مقیاسبندی زمانهای انتظاری داشت که قبلاً توسط ETAS نسبت داده شده بود [9,10] و البته از مطالب اساسی جدیدی نیز برخوردار بود. به جای قانون توان اول با یک نوک نمایی (توزیعِ از نوع گاما) توزیعهای بدست آمدهی آنها با ترکیب قانون توان دوم سازگاری داشت. در نمودار دو-لگاریتمی (double-logarithmic) این موضوع به شکل توزیع پای-سگ (dog-leg) نمایان میشود: منحنی تشکیل شده از دو قطعه با شیبهای مختلف که شبیه پای عقبی یک سگ است. تحت شرایط پایا٬ مدلِ ETAS توزیع گامایی را تولید میکند که از ترکیب رویدادهای اتفاقی زمینه و پسلرزههای تصحیحیافته نتیجه میشود [9,10]. بارو و همکارنش نشان دادند که قانون پای-سگ به جای آن٬ ناشی از غیرپایایی موجود در آهنگ رویدادهای زمینه است. بحث آنها این بوده که منشاء ناپایایی در دو مورد متفاوت است. در آزمایشگاه این ناپایایی شتاب غیرخطی در آهنگ زمینه به عنوان یک تنش در زمان٬ افزایش می یابد و برای زمینلرزهها عمدتاً در اثر تغییرپذیری در آهنگ زمینهای است که به خوشهبندیِ مکانی مربوط است.
نتایج آزمایشها و کارهای تیمِ بارو نشان از این موضوع میدهد که مدلِ ETAS میتواند در تمامیِ مقیاسها از عهدهی مسائل مربوط به لرزهشناسی برآید. این مدل میتواند به توسعهی بهترِ پیشگوییهای احتمالی در مورد زمینلرزهها و دیگر مخاطرات همچون رانشِ زمین و آتشسوزیِ جنگلها نیز کمک شایانی کند. با این وجود تنها آزمایشهای گسترده با مشاهداتِ آینده است که از قدرت واقعی پیشبینیِ این رهیافت پرده برخواهد داشت و زمینه را برای هدایت آن بهسوی سیاستها و تصمیمات عملیاتی فراهم خواهد کرد.
دربارهی نویسنده:
ایان ماین (Ian Main) استاد لرزهشناسی و فیزیک سنگ در مدرسهی علومزمینی در دانشگاه ادینبرگ است.
مراجع:
- C. H. Scholz, L. R. Sykes, and Y. P. Aggarwal, “Earthquake Prediction: A Physical Basis,” Science 181, 803 (1973).
- S. Hough, Predicting the Unpredictable: The Tumultuous Science of Earthquake Prediction (Princeton University Press, Princeton, 2009)[Amazon][WorldCat].
- P. Bak, How Nature Works: The Science of Self-Organised Criticality (Oxford University Press, Oxford, 1997)[Amazon][WorldCat].
- I. Main, “Statistical Physics, Seismogenesis, and Seismic Hazard,” Rev. Geophys. 34, 433 (1996).
- http://www.nature.com/nature/debates/earthquake/equake_frameset.html.
- M. Huc and I. G. Main, “Anomalous Stress Diffusion in Earthquake Triggering: Correlation Length, Time Dependence, and Directionality,” J. Geophys. Res. 108, 2324 (2003).
- J. Baró, Á. Corral, X. Illa, A. Planes, E. K. H. Salje, W. Schranz, D. E. Soto-Parra, and E. Vives, “Statistical Similarity between the Compression of a Porous Material and Earthquakes,” Phys. Rev. Lett. 110, 088702 (2013).
- Y. Ogata, “Statistical Models for Earthquake Occurrences and Residual Analysis for Point Processes,” J. Am. Stat. Assoc. 83, 9 (1988).
- A. Saichev and D. Sornette, “Theory of Earthquake Recurrence Times,” J. Geophys. Res. 112, B04313 (2007).
- S. Touati, M. Naylor, and I. G. Main, “The Origin and Non-Universality of the Earthquake Inter-Event Time Distribution,” Phys. Rev. Lett. 102, 168501 (2009).
- T. Jordan, Y. Chen, P. Gasparini, R. Madariaga, I. Main, W. Marzocchi, G. Papadopoulos, G. Sobolev, K. Yamaoka, and J. Zschau, “Operational Earthquake Forecasting: State of Knowledge and Guidelines for Utilization,” Ann. Geophys. 54, 361 (2011).
منبع:
نویسنده خبر: بهنام زینالوند فرزین
کد خبر : 925
آمار بازدید: ۳۵۱
آمار بازدید: ۳۵۱
«استفاده از اخبار انجمن فیزیک ایران و انتشار آنها، به شرط
ارجاع دقیق و مناسب به خبرنامهی انجمن بلا مانع است.»
ارجاع دقیق و مناسب به خبرنامهی انجمن بلا مانع است.»
حامیان انجمن فیزیک ایران (به حامیان انجمن بپیوندید)
 RSS
RSS