یافتن مدارهای مربوط به یک سیستم سهجسمی که تحت گرانش متقابل خود هستند، همواره یکی از پرسشهای دشوار فیزیک بوده است. به تازگی، گروهی از پژوهشگران با استفاده از شبیهسازی عددی توانستند، دستهی جدیدی برای انواع این مدارها پیدا کنند.
برای محدودهی وسیعی از شرایط اولیه، پاسخ یک سیستم دوجسمی به گرانش متقابلی که بین آنها وجود دارد، یک مدار بیضوی ساده است. اما اضافه کردن یک جسم بیشتر و یا شرایط اضافهی دیگر، مسئله را دشوار میکند و در حالت کلی توصیف سادهی ریاضی را با چالش مواجه میکند. یک حالت خاص، که در آن سه جسم در رأسهای یک مثلث٬ در حال چرخش هستند٬ دو قرن پیش توسط لاگرانژ مشخص شده است. اما تنها پس از دهه هفتاد و نود میلادی بود که پژوهشگران دو گونه دیگر از حرکات نوسانی یک سیستم سه جسمی را کشف کردند.
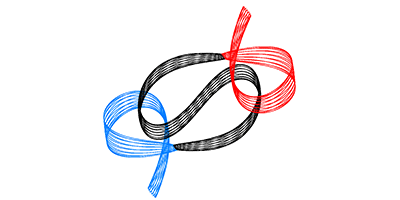
M. Šuvakov and V. Dmitrašinović, Phys. Rev. Lett. 2013
به تازگی در مجله Physical Review Letters میلوان سواکوف (Milovan Suvakov) و ولکو دمیتراسینوویچ (Veljko Dmitrasinovic) از مؤسسه فیزیک بلگراد در صربستان٬ توانستند ۱۳ دستهی دیگر از مدارهای نوسانی برای یک سیستم سهجسمی با جرمهای یکسان٬ که تحت تأثیر گرانش در یک صفحه در حرکت اند را، کشف کنند. برای دسته بندی این مدارها٬ که با شبیهسازی عددی نشان داده شدهاند٬ سواکوف و دمیتراسینوویچ٬ تحلیلهای قبلی را توسعه دادند. در این روش توسعه، ساختار بهدست آمده از چیدمان مثلثی، به طور ریاضی، توسط یک نقطه بر روی کره نمایش داده شدهاند. مدارهای فیزیکی، متناظر با مسیرهای بسته بر روی کره هستند. در این مسیرها از نقاط برخورد که در آن دو جسم در یک نقطه یکسان هستند، پرهیز شده است. با بهرهگیری از این طرح تقسیمبندی توپولوژیکی٬ نویسندگان این مقاله توانستهاند تا مدارهای مختلف را با تعداد دفعههایی که این مدارها به صورت ساعت گرد و پادساعتگرد حول نقاط ممنوع(نقاط برخورد) گردش میکنند متمایز کنند. از بین این ۱۳ دسته از حرکت نوسانی که آنها کشف کرده اند٬ سه تا از آنها به حلهای قبلی مرتبط میشوند اما دهتای آنها کاملاً در دستهی جدید قرار میگیرند. (مجموعهای از مسیرها در اینجا نمایش داده شدهاند).
تجسم حرکتهای پیچیده سخت است٬ و این مدارها در طبیعت تنها برای شرایط اولیه خاص اتفاق میافتند. اما این حلهای خاص، به پژوهشگران کمک میکند تا مسئله پیچیده سهجسمی را بهتر بفهمند.
مرجع
http://physics.aps.org/synopsis-for/10.1103/PhysRevLett.110.114301
منبع